
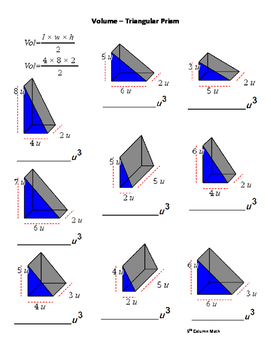
These are the two most fundamental equations: volume 0.5 b h length. Then use it to estimate the volume lost to one indentation and multiply it by their number to get the actual chocolate filled volume. The triangular prism volume (or its surface area) is usually what you need to calculate. Find the volume of a triangular prism whose base is 16 cm, height is 9 cm, and length is 21 cm.
Volume of triangular prism calculator free#
One way to approach this curious problem is to first use the volume of a prism calculator above to calculate the volume of the bar, including the indentations. Triangular Prism Calculator is a free online tool that displays the surface area and the volume of the triangular prism. The formula to calculate the volume of a triangular prism is given below: Volume (V) 1/2 × b × h × l, here b base edge, h height, l length Let us solve an example to understand the concept better.

Many camping tents are also such prisms, making use of the same beneficial properties.Ī triangular prism volume calculation may also be handy if you want to estimate the volume of a toblerone bar. This type of roof has the best distribution of forces generated by the weight of the roofing and lateral forces (i.e.
Volume of triangular prism calculator how to#
J 644K subscribers Subscribe 2.1K 182K views 1 year ago Volume Welcome to How to Find the Volume of a Triangular. To calculate the volume of a triangular prism you can use the formula for all prisms, where the area of the base is multiplied by its length. Practical applicationsĪ lot of classical roofs have the shape of a triangular prism, so calculating the volume of air below it might be useful if you are using the space as a living area. How to Find the Volume of a Triangular Prism Math with Mr.
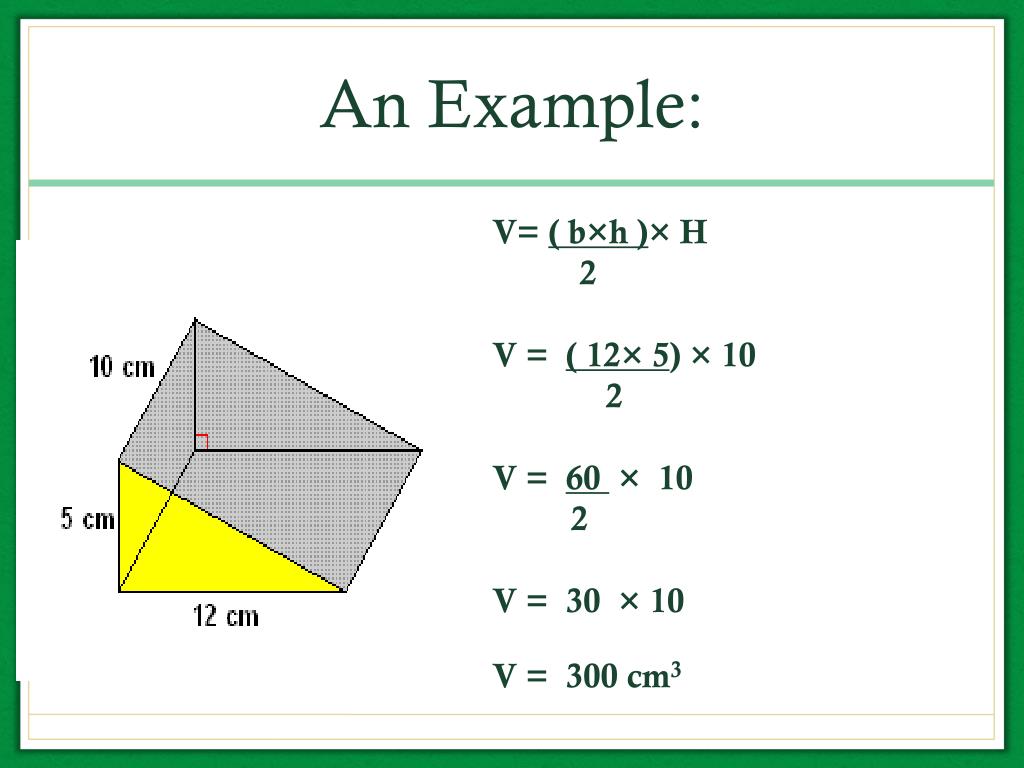
We want to be able to find the net and calculate the volume and surface area for different types of prisms, like rectangular, triangular, etc. For example, if the height is 5 inches, the base 2 inches and the length 10 inches, what is the prism volume? To get the answer, multiply 5 x 2 x 10 and divide the result by 2, getting 10 x 10 / 2 = 100 / 2 = 50 cubic inches. In this lesson we’ll look at an introduction to three-dimensional geometric figures, specifically nets, volume, and surface area of prisms. Three measurements of a prism need to be known before the volume can be calculated using the equation above: the prism length, height, and base.


 0 kommentar(er)
0 kommentar(er)
